下圖為高層建築斷面及順風向、橫風向、扭轉向座標示意圖。

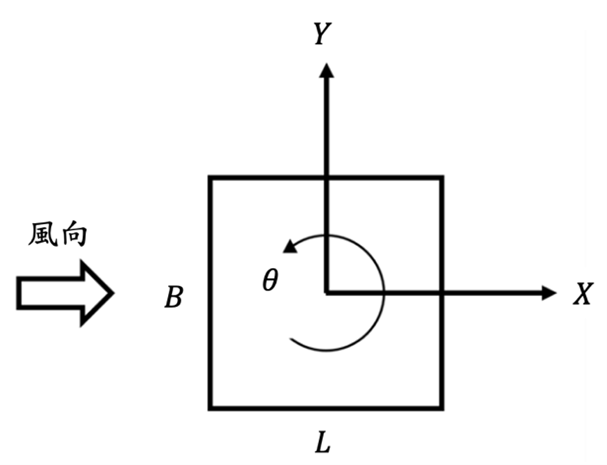
圖 C5.1 順風向、橫風向及扭轉向座標示意圖

計算順風向加速度、橫風向加速度及扭轉向加速度時，僅需考慮回歸期為一年的風速作用下，所產生共振部分風力的影響。令 $D^\ast$、$L^\ast$、$θ^\ast$ 分別是在回歸期為一年的共振部分風力作用下，經結構分析所得建築物最高居室樓層之順風向、橫風向與扭轉向位移，則建築物最高居室樓層形心位置之順風向最大加速度 $A_D$、橫風向最大加速度 $A_L$ 與扭轉向最大加速度 $A_T$，分別為：

其中計算 $D^\ast$、$L^\ast$、$θ^\ast$ 所需之 1 年回歸期共振部分風力依下列方式計算。

(1) 當建築物之高寬比滿足 $3\le h/\sqrt{BL}\le6$，在回歸期為一年的風速作用下，高度 $z$ 處之順風向、橫風向及扭轉向共振部分風力，可依下列計算式求得：

i. 順風向共振部分風力依 3.2節 之規定計算，但其中陣風反應因子應使用僅包含共振部分之 $\bar{G}$ 如下：

ii. 橫風向共振部分風力依 式(C5.3) 計算，其中之參數依 3.6節 之規定計算。

iii. 扭轉向共振部分風力依 式(C5.4) 計算，其中之參數依 3.7節 之規定計算。

(2) 當建築物之高寬比滿足 $h/\sqrt{BL} < 3$，在回歸期為一年的風速作用下，高度z處之順風向、橫風向及扭轉向共振部分風力，可依下列計算式求得：

i. 順風向共振部分風力依 3.2節 之規定計算，但其中陣風反應因子應依 式(C5.2) 計算。

ii. 橫風向共振部分風力依 式(C5.5) 計算，$W_{Lz}$ 為回歸期一年風速作用下，依據 式(3.15) 所得之 $z$ 處高度橫風向風力。

iii. 扭轉向共振部分風力依 式(C5.6) 計算，$M_{Tz}$ 為回歸期一年風速作用下，依據 式(3.22) 所得之 $z$ 處高度扭轉向風力。

建築物角隅處之順風向、橫風向與扭轉向振動加速度之組合

最高居室樓層角隅之振動尖峰加速度值之計算，是基於順風向振動與橫風向及扭轉向振動不相關，橫風向振動與扭轉向振動完全相關的條件下為之。

假設順風向振動與扭轉向振動之間為不相關，則建築物角隅處之順風向振動加速度為：

瞬時加速度：

加速度變異數：

假設橫風向振動與扭轉向振動之間為完全相關，則建築物角隅處之橫風向振動加速度為：

瞬時加速度：

加速度變異數：

建築物角隅處之水平方向振動加速度均方根值，$\sigma_A$，可寫為：

建築物角隅處之水平方向振動尖峰加速度，$\widetilde{A}$，為：

其中 $\widetilde{g}$ 為對應角隅處之水平方向振動的尖峰因子。$\widetilde{A}$ 亦可用下式計算之：