參考＜風工程＞（五南出版，2020，蕭葆羲），當大氣狀況條件為中性 (neutral)，亦即大氣垂直向之溫度梯度 (temperature gradient) 等於絕熱傾率 (adiabatic lapse rate)，且由於地面粗糙摩擦影響，使得吹過地面之風呈現紊流 (turbulence) 流況，同時在地表面形成一邊界層 (boundary layer)，稱為中性大氣紊流邊界層 (neutral turbulent boundary layer)。關於中性大氣紊流邊界層之風場特性描述，一般主要參數包括有：平均風速剖面、紊流強度剖面、紊流積分長度尺度、雷諾應力 (Reynolds stress) 剖面、與紊流風速頻譜 (fluctuating velocity spectrum) 等。在風工程相關問題之設計、評估、與應用上，這些風場特性參數均為不可或缺，非常重要。平均風速剖面在 2.2 節 中已有解說，以下針對其他風場特性說明之。

紊流強度係代表風場流速擾動大小的強弱 (即紊流動能大小) 之一種指標。其與地表粗糙度、距地面高度以及大氣穩定度有關。一般而言，隨大氣不穩定及地表粗糙度增加而變大。根據 Counihan(1975) 指出，中性大氣邊界層內的紊流強度有以下的特性：

式(2.2) 所表示的紊流強度為主流向隨著高度 $z$ 變化的紊流強度。依本規範評估設計風力、設計風壓、及頂樓角隅加速度，或採用風洞試驗或電腦數值模擬時，此參數為風場特性主要考量因素之一。

風之紊流可視為由許多大小不同之渦漩 (eddy) 所組成。利用積分方式，可求得紊流積分尺度 (integral scales)。可視該積分值為紊流渦漩之平均特性。積分尺度包括時間尺度及長度尺度，其中積分長度尺度 (integral length scale) 可當做渦漩之平均大小尺寸，而積分時間尺度 (integral time scale) 則為平均尺寸渦漩旋轉一圈所需時間。紊流積分長度尺度基本上可視為量度組成紊流之渦漩之平均尺寸。若採用卡式座標(主流向 $x$、側向 $y$、垂直向 $z$)，並考慮三方向之擾動速度 (主流向 $u^{'}$、側向 $v^{'}$、垂直向 $w^{'}$)，則紊流積分尺度將包含九個分量，$L_x^u$、$L_y^u$、$L_z^u$、$L_x^v$、$L_y^v$、$L_z^v$、$L_x^w$、$L_y^w$、$L_z^w$。關於中性大氣邊界層內不同高度 $z$ 之紊流積分尺度，Counihan(1975) 建議在 $z = 10～240$ 公尺範圍內，$L_x^u$ 與高度 $z$ 關係經驗式為：

其中 $c$ 與 $m$ 可由下圖曲線獲得。$z_0$ 為粗糙長度，一般來說，鄉村開闊地況約為 0.003～0.2 $m$ 之間；鄉鎮市郊地況約在 0.2～1 $m$ 之間；都會地況約在 1～4 $m$ 之間。 式(2.2) 中之 $L_x^u$ 多用以表示風場主要特性之一，可視為 式(2.3) 的 $L_z$。

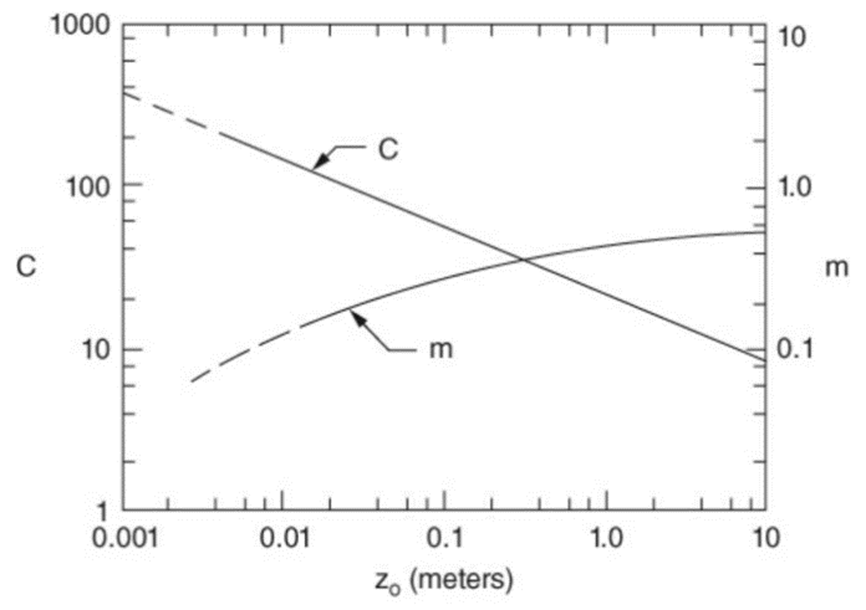
圖 C2.1 紊流積分長度尺度參數

式(2.3) 所表示的紊流積分尺度為主流向隨著高度 $z$ 變化的積分長度尺度。依本規範評估設計風力、設計風壓、及頂樓角隅加速度，或採用風洞試驗或電腦數值模擬時，此參數為風場特性主要考量因素之一。

雷諾應力 (Reynolds stress) 係為大氣邊界層紊流中之剪應力 (shear stress) 現象，該應力與地表粗糙度有相當密切的相關性。假設主流向擾動風速為 $u^{'}$、側向擾動風速為 $v^{'}$、垂直向擾動風速為 $w^{'}$，則雷諾應力為任兩向擾動風速之相關性 (correlation)，以變異數表示之。雷諾應力分量共計有九個，分別為 $\overline{u^{'}u^{'}}$、$\overline{u^{'}v^{'}}$、$\overline{u^{'}w^{'}}$ 、$\overline{v^{'}u^{'}}$、$\overline{v^{'}v^{'}}$、$\overline{v^{'}w^{'}}$、$\overline{w^{'}u^{'}}$、$\overline{w^{'}v^{'}}$、$\overline{w^{'}w^{'}}$。此處” $\overline{ }$ ”表示為時間平均。九個分量中 $\overline{u^{'}u^{'}}$、$\overline{v^{'}v^{'}}$、$\overline{w^{'}w^{'}}$ 較小，而另外六個兩兩相同，故實際上常以 $\overline{u^{'}v^{'}}$、$\overline{v^{'}w^{'}}$、$\overline{u^{'}w^{'}}$ 為代表。根據 Counihan(1975) 研究，鄉村地區的 $\overline{u^{'}w^{'}}/{U_\infty^2}$ 比值約在 0.002 至 0.0025 之間，${U_\infty}$ 為邊界層梯度的自由流速；市郊地區的 $\overline{u^{'}w^{'}}/{U_\infty^2}$ 比值約為 0.0025；都市地區的雷諾應力與鄉村地區的雷諾應力比值則在 1.46～1.56 之間。一般大氣邊界層在地面 50～100 公尺高度之內，雷諾應力幾乎為定值，在這等應力值之範圍稱為等應力層 (constant stress layer)。

風具有紊流現象且可視為由許多大大小小各種不同尺度之渦漩所組成，而各種尺度可依其頻率高低來表示，故理論上可以將紊流能量依照不同頻率範圍來瞭解渦漩能量分配情形，此稱為紊流能譜或擾動風速頻譜。如 圖 C2.2 所示，可將紊流能譜依頻率分為三個部分：(1)低頻部分之含能渦漩區 (energy containing eddies)、(2)中頻部分之慣性次階區 (inertial subrange)、(3)高頻部分之黏滯消能區 (viscous dissipation)。

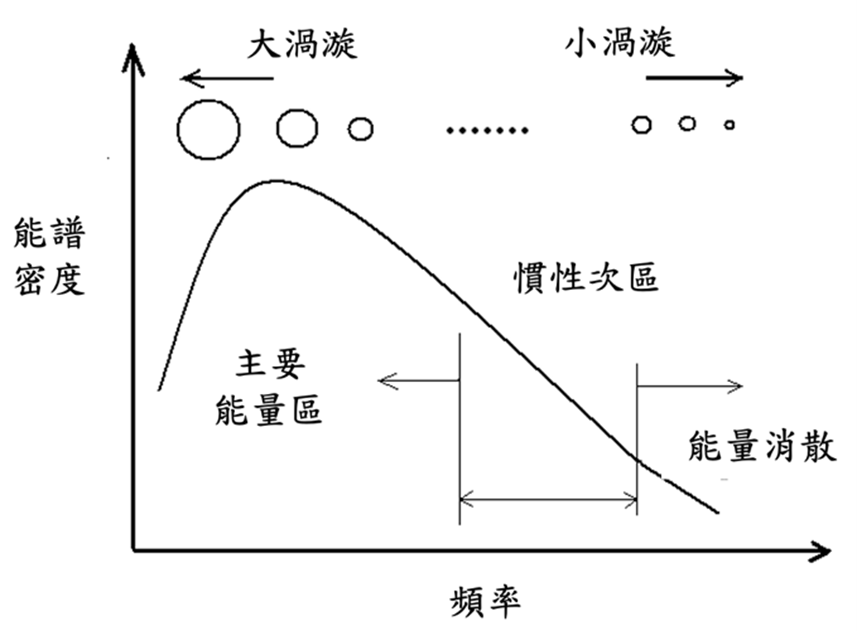
圖 C2.2 紊流能譜示意圖

紊流之能量傳輸，基本上是由低頻部分之大尺度渦漩抽取平均流之動能，再經由慣性次階向高頻部分之消能區傳遞，以提供邊界處黏滯摩擦效應所需損耗之能量。其中低頻部分含最大尺度之渦漩，為支撐紊流動亂之主體。關於紊流能譜分佈，依據Kolomogrove理論與假設，可推導出慣性次階區之能譜關係式：

式中 $S\left(n\right)$ 為能頻密度或頻譜密度 (power spectral density) 函數；$\varepsilon$ 為紊流能量消耗率 (energy dissipation rate)；$n$ 為紊流頻率。常見的能頻密度公式，以 von Karman(1948) 及 Eurocode 所提出之無因次化能譜密度為主，分別為下面兩式：

其中 $S_u(z,n)$ 為 $z$ 高度處之主流向紊流能譜密度；$\overline{u^{\prime2}}$ 為 $z$ 高度處之風速擾動均方根值；$L_z$ 為 $z$ 高度處之紊流積分長度尺度；$U_z$ 為 $z$ 高度處之平均風速。

中性大氣邊界層中，空間中兩點間的擾動風速在不同頻率範圍有不同程度的相關性。一般來說，距離較遠的兩點位置擾動風速具有較低的相關性，距離較近的兩點則具有較高的相關性。位於兩點1、2的交頻譜密度可表示為：

其中 $i=\sqrt{-1}$；$r$ 為兩點位置相對距離；$S_{u_1u_2}^C\left(r,n\right)$ 為共同頻譜密度；$S_{u_1u_2}^Q\left(r,n\right)$ 為正交頻譜密度。一般交頻譜密度可用交相關函數來取代：

Davenport(1968) 針對 y-z 平面上兩點間的交相關函數提出以下經驗公式：

其中 $y_1$ 與 $y_2$ 為兩點在側向位置；$z_1$ 與 $z_2$ 為兩點在垂直向位置；$U_{z_1}$ 與 $U_{z_2}$ 為兩點在 $z_1$ 與 $z_2$ 高度上的平均風速。

採用風洞試驗方法時，擾動風速的紊流特性包含能頻密度、交頻譜密度等，均可為流場模擬用以驗證的風場特性指標。